딥러닝으로 XOR 문제 풀기
# XOR 문제
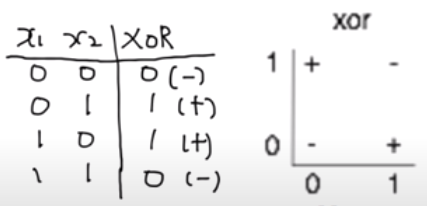
XOR 문제는 두 변수 x1, x2가 같다면 False를, 다르다면 True를 반환하는 문제이다. 많은 Neural Network 연구자들이 이 문제를 해결하기 위해 애썼지만, 이 문제는 하나의 유닛으로는 해결할 수 없다는 것이 수학적으로 증명될 정도로 해결하기 어려웠고 ‘Neural Network는 안된다’는 인식이 강해졌다. 이후 여러 개의 유닛을 사용하면 XOR 문제를 해결할 수 있음이 알려졌지만 어떻게 매개변수 w, b를 학습할 수 있을지에 대해 다시 한번 장벽에 부딪혔다. 하지만, 결국 Neural Network는 XOR 문제를 극복해냈는데 지금부터 어떻게 이것이 구현됐는지 살펴보고자 한다.
# Neural Network로 XOR 문제 해결하기
1. Forward Propagation
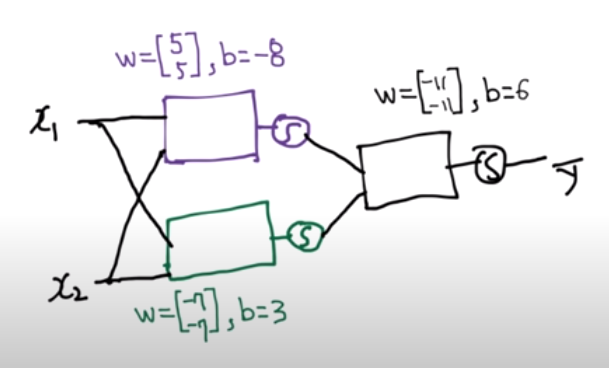
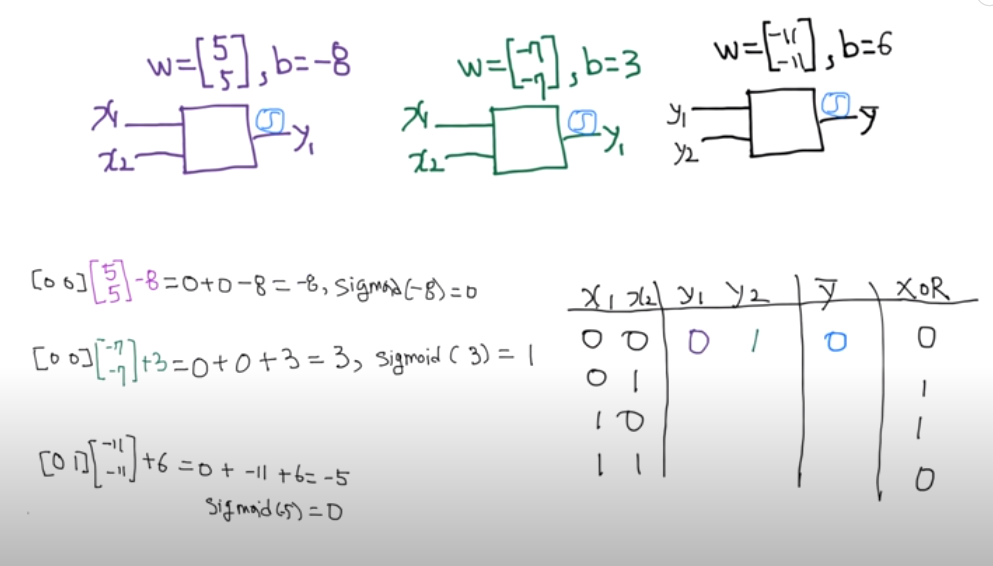
왼쪽 그림은 세 개의 유닛을 쌓아 만든 간단한 Neural Network 모델이다. 이 모델을 이용하면 XOR 문제를 해결할 수 있는데, 오른쪽 그림처럼 모델 유닛들의 가중치 w와 편향 b가 주어지면 XOR 문제에서 주어진 x1, x2를 모델에 입력하여 결과를 계산할 수 있다. 첫 번째 유닛은 행렬 연산을 수행하면 -8이라는 값이 나오고 이를 시그모이드(sigmoid) 함수에 넣으면 0에 매우 근접한 값 y1을 얻을 수 있다. 두 번째 유닛도 같은 방식으로 계산해 1에 매우 근접한 값 y2를 얻을 수 있으며, 계산을 통해 y1, y2를 세 번째 유닛에 넣고 계산하면 XOR 문제가 요구하는 답인 0을 얻을 수 있다.


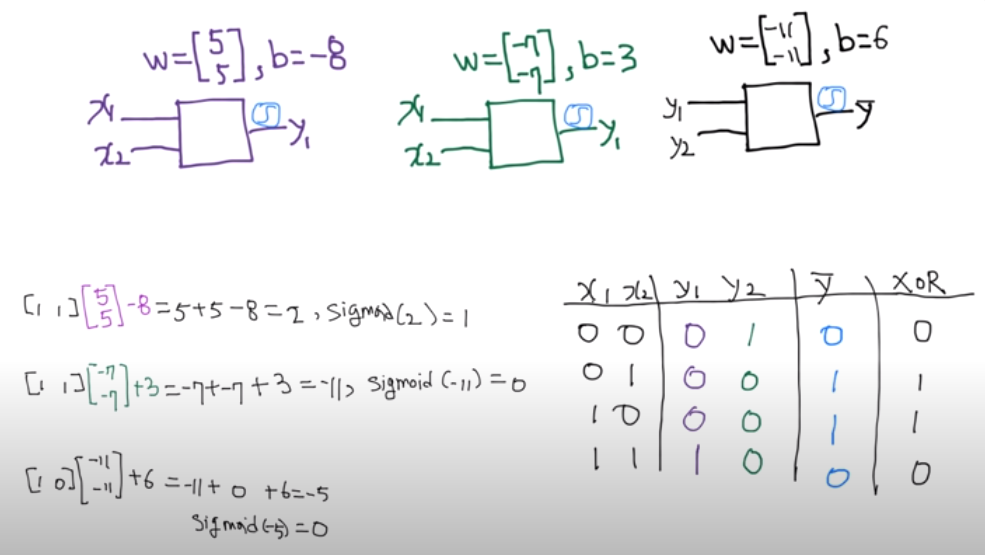
나머지 XOR 문제도 같은 Neural Network로 연산하면 XOR 문제를 해결하기 위한 답을 도출할 수 있다. 이렇게 주어진 모델에 input을 넣고 output을 출력해내는 과정을 Forward Propagation이라고 한다.
2. Back Propagation
앞선 예시의 경우 Neural Network 모델의 w, b가 주어진 상태로 연산을 진행했다. 사실 단순한 얕은 Neural Network의 경우 XOR 문제를 해결할 수 있는 w, b를 사람이 직접 찾을 수 있다. 하지만 더욱 깊은 Neural Network의 경우 w, b를 직접 찾는 것은 불가능하다. 그렇다면 w, b가 주어지지 않았을 때는 어떻게 모델을 학습하여 w, b를 자동적으로 계산해낼 수 있을까?
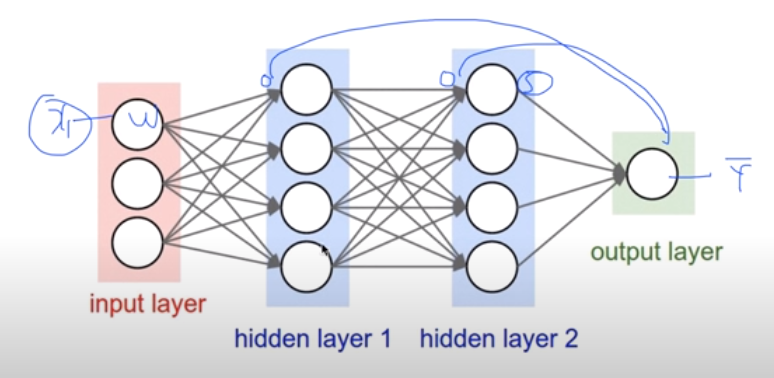
가중치 w, 편향 b를 자동적으로 계산해내기 위해서는 Gradient Descent 알고리즘이 필요하다. 이를 위해 미분을 통해 기울기를 구하는 작업이 동반된다. 그러나 가중치를 조정하기 위해서는 네트워크 각 layer의 input들이 output y에 미치는 영향을 알아야 하는데, 깊은 네트워크일수록 x에 대한 미분을 구하기가 어려워 x가 y에 미치는 영향을 파악하기 힘들다. 심지어 MIT AI Lab의 Marvin Minsky 교수는 Perceptrons(1969)에서 아무도 이것을 학습시킬 수 없다고 말하며 당시 Neural Network의 암흑기가 도래했다.

이러한 학습의 난관을 Paul Werbos가 논문을 통해 Backpropagation 방법을 제시하며 해결했다. 당시에는 Neural Network가 주목받지 못해 Paul의 논문은 조명받지 못했지만, 사장됐던 Backpropagation을 Geoffrey Hinton 교수가 자신의 방법으로 다시 제안하며 Neural Network는 다시 관심을 받게 되었다.
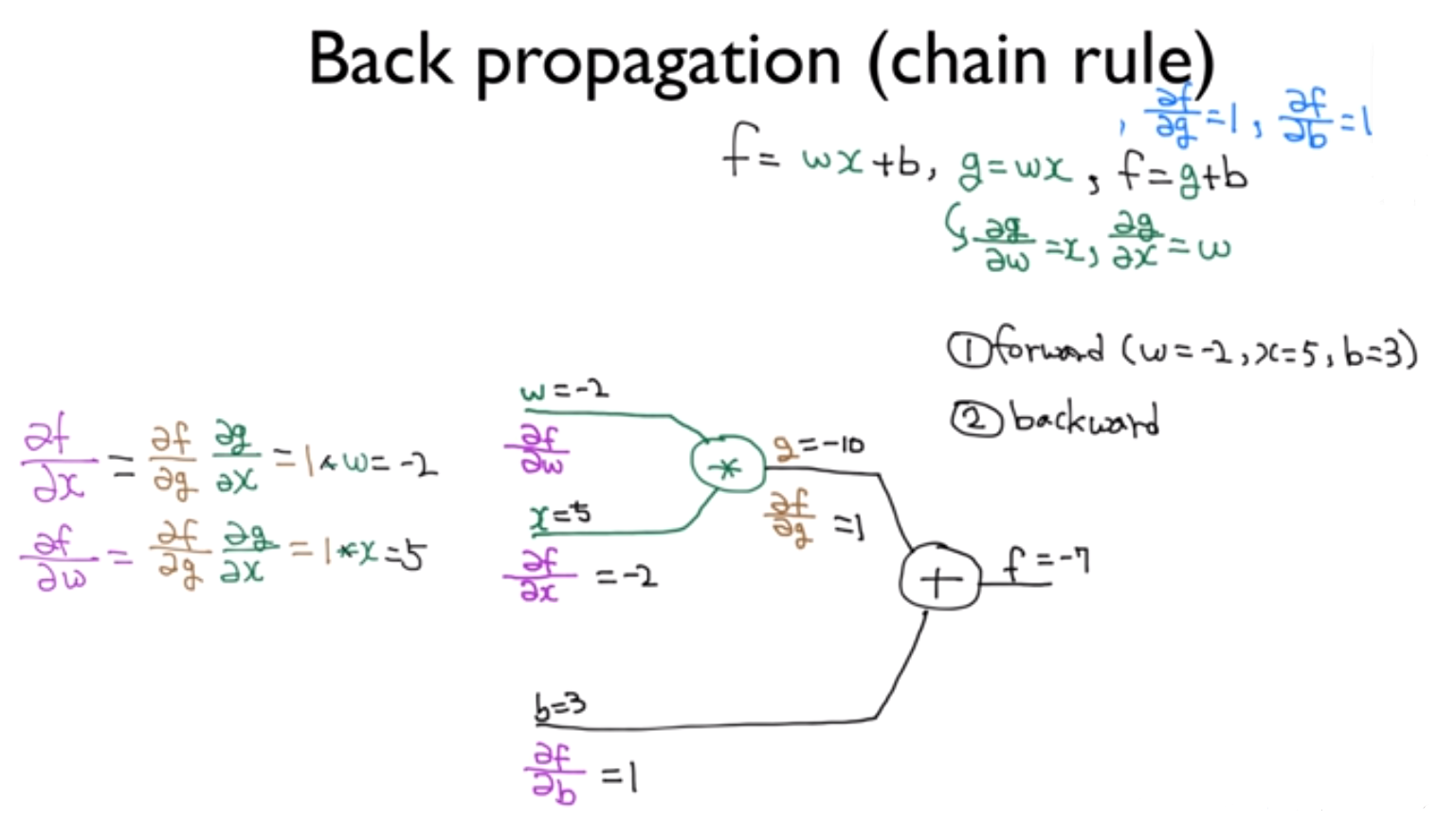
그들이 제시한 Backpropagation은 예측값과 실제값 사이의 오류(Error)를 Cost 함수를 이용해 뒤에서부터 앞으로 보내 미분값을 구하고 w, b를 어떻게 수정할지 계산하는 방법이다. 여기에서는 미분의 공식 중 하나인 chain rule이 강력한 도구로 활용된다. 위 그림 같이 f 함수를 g 함수와 b에 대하여 미분한 값들과 g함수를 w와 x에 대해 미분한 값들을 단순히 계산해내면, chain rule을 통해 f 함수를 w와 x에 대해 미분한 값들을 쉽게 구해낼 수 있게 된다.
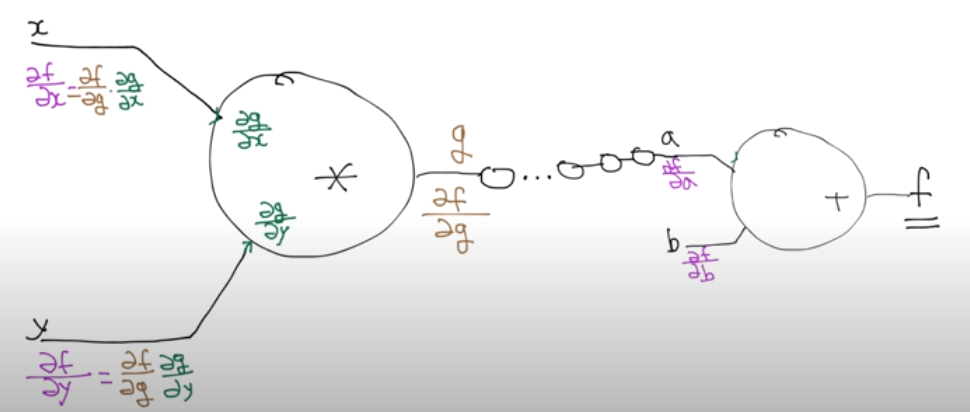
네트워크의 layer가 매우 많은 모델에 대해서도 chain rule을 통해 하나하나 미분값을 알아내가면 결국 위 그림처럼 f를 x, y에 대해서 각각 미분한 값들을 알아낼 수 있게 되고, 결국 w, b에 대해서도 미분값을 알아내어 Gradient Descent를 실행할 수 있게 된다. 이러한 Backpropagation은 매우 깊은 네트워크도 충분히 학습 가능하게 하는 딥러닝의 강력한 도구이다.
ReLU 함수
# Backpropagation에서 나타나는 Vanishing gradient 문제

모델의 층을 많이 쌓을수록 보다 다양한 문제를 풀 수 있지만, backpropagation을 하며 input이 output에 미치는 영향을 알아볼 때 chain rule을 통해 얻은 미분값이 너무 작아져 학습이 잘 안되는 문제가 생긴다.

위와 같이 곱셈에 대한 오차역전파를 구할 때 x에 대한 g(x)의 미분 값은 y가 되는데, y는 시그모이드 함수를 통과한 출력 값이라 범위가 0~1 사이로 고정된다. 만일 x = -10이어서 y가 0에 근접한 수를 갖게 된다면, x에 대한 f(x)의 미분값은 g(x)에 대한 f(x)의 미분값 곱하기 y이기 때문에 0에 근접한 값을 갖게 된다. 이러한 과정을 계속 반복해 더욱 0에 가까운 값으로 경사하강법을 수행하면 매개변수 w와 b의 학습이 제대로 이뤄지지 않게 된다. 이러한 문제를 경사도가 사라진다는 의미에서 Vanishing gradient라고 한다.
이 Vanishing gradient 문제로 인해 2~3단계를 넘어가는 층을 가진 Neural Network는 학습시킬 수 없다는 좌절에 빠지게 되고, Neural Net은 1986년~2006년까지 2차 겨울을 맞이 하게 된다.
# ReLU (Rectified Linear Unit) 함수

Geoffrey Hinton 교수는 Vanishing gradient의 원인을 시그모이드 함수에서 찾았다. (We used the wrong type of non-linearity) 시그모이드 함수는 항상 1 미만의 값을 갖는 한계점이 있기 때문에, 입력이 0 이하인 범위에서는 y = 0 함수를 갖고 입력이 0 초과인 범위에서는 y = x 함수를 갖는 ReLU 함수를 시그모이드 함수의 대안으로 제시했다.
Neural Net에서 Activation function으로 단순히 ReLU를 사용하면 해당 network의 학습을 원할하게 진행시킬 수 있다. 즉 층이 2~3 층정도로 적은 모델의 경우 기존의 시그모이드를 사용해도 괜찮지만, 이보다 더 많은 층수를 가진 모델은 ReLU를 사용해야 학습 진행이 가능하다.

실제로 Neural Net에 ReLU 함수를 적용 시, 미동이 없는 시그모이드에 비해 ReLU가 빠르게 Cost 함수를 줄여나가는 것을 관찰할 수 있다.

ReLU 함수에서 더 나아가 Leaky ReLU, tanh, Maxout, ELU 등의 다양한 activation 함수들이 존재하고 상황에 따라 효과적인 함수를 선택해 사용할 수 있다.

위의 activation 함수들을 각각 사용하여 CIFAR-10 이미지 데이터에 대한 정확도를 측정해본 결과, 실제로 시그모이드를 제외한 다른 activation 함수들은 큰 문제없이 높은 정확도를 기록하는 모습을 살펴볼 수 있다.
Weight initialization
# 가중치 초기화 (Weight initialization)
1. Zero initialization

Geoffrey Hinton 교수가 찾아낸 Neural Network가 제대로 동작하지 않는 이유들 중 하나는 가중치 초기화의 문제이다.
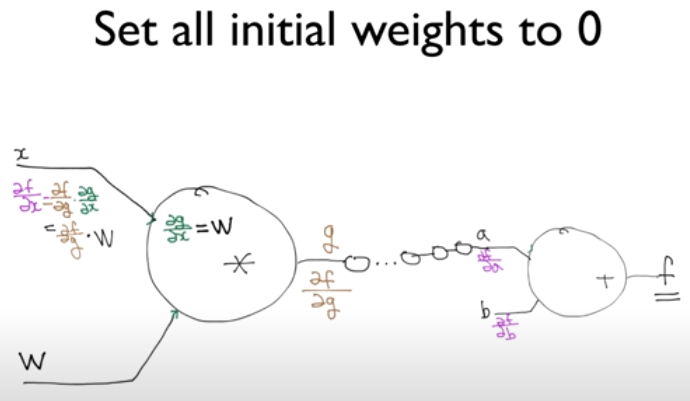
예를들어, 극단적으로 가중치를 0으로 초기화하면 backpropagation으로 구한 x에 대한 f(x)의 기울기 값이 0이 되어 기울기가 소실되는 현상이 발생한다. 이 경우 학습이 원활하게 이뤄지지 않기 때문에, 가중치 초기화의 첫번째 유의점은 ‘w를 모두 0으로 설정하지 말자.’이다.
2. RBM을 이용한 initialization
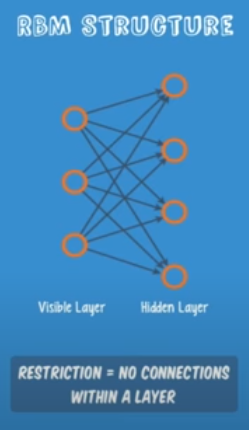
가중치를 어떻게 설정해야할 지에 대한 문제는 깊이 들어갈수록 어려워졌는데, Hinton 교수는 A Fast Learning Algorithm for Deep Belief Nets (2006)이라는 논문을 통해 RBM(Restricted Boatman Machine)으로 Neural Network의 가중치를 초기화하자고 제안했다. RBM을 사용해 가중치를 초기화한 Neural Net을 Deep Belief Nets이라고 한다.
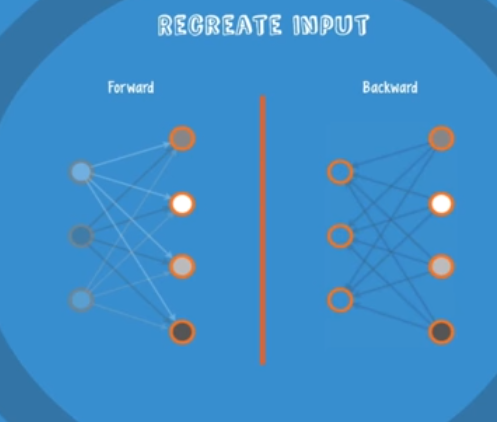
RBM이란 Input을 모델에 넣어 Output을 구하고 (encoder), 구한 Output 값에 다시 가중치를 곱하여 Input 값을 예측해낸 뒤 (decoder), 원래의 Input 값과 예측한 Input 값의 차가 최저가 되도록 (두 값이 거의 동일해지도록) 가중치를 조정해나가며 초기값을 설정하는 방법이다.
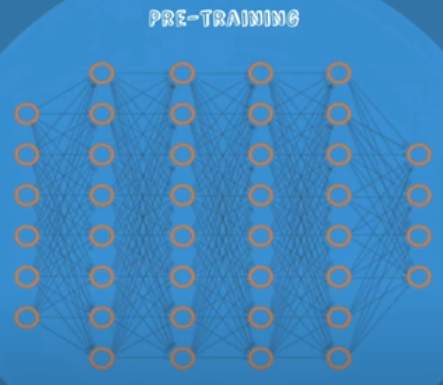
전체 네트워크에 대해 RBM을 사용해 가중치를 학습시키는 것을 Pre-Training이라고 한다. 이것을 구현하기 위해 먼저 인접한 첫 번째와 두 번째 레이어에 대해 encoder와 decoder로 값을 비교하여 가중치를 학습시키고 다음 인접한 두 번째, 세 번째 레이어에 대해서도 똑같은 과정을 반복하며 네트워크의 끝까지 모든 레이어에 대해 가중치를 학습시킨다.
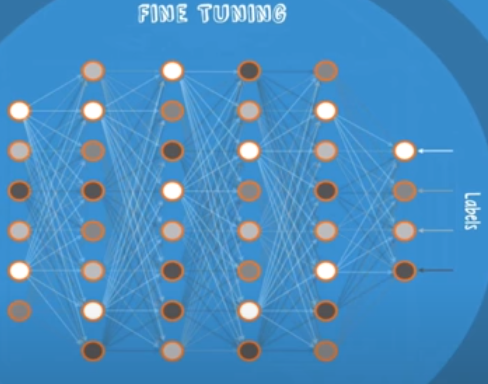
Pre-Training을 거쳐 가중치를 초기화한 모델을 원래대로 training data를 주고 학습시키는 것을 특별히 Fine Tunning한다고 말한다. Pre-Training을 통해 이미 가중치들이 생각보다 잘 학습되어서 좋은 초기값을 제공하므로 살짝의 튜닝만 한다는 의미에서 training 과정을 다르게 지칭한다.
3. 더욱 simple한 초기화

RBM을 사용해 가중치를 초기화하는 과정을 하나하나 거쳐가는 것은 복잡하다. 초기화 과정을 더욱 간단하게 진행하기 위해 Xavier initialization, He initialization 등의 초기화가 등장했다. 이 두 방법은 input 값의 개수와 output 값의 개수를 고려하여 초기화를 진행하는 방법인데, 위 식과 같이 초기화를 진행하면 RBM을 사용한 것과 동일한 혹은 더 나은 성능을 보여준다고 알려져 있다. 흥미로운 점은 He initialization이 Xavier initialization의 식에서 단순히 분모 루트 안의 값을 2로 나눠주는 것으로 Xavier initialization보다 더 좋은 성능을 보여준다는 사실이다.
이러한 가중치 초기화에 대한 연구는 아직도 활발히 진행 중이므로 여러가지 초기화 방법에 대해 알아두고 데이터마다 다르게 적용해볼 필요가 있다.
Dropout과 Ensemble
# Overfitting 문제

뉴럴 넷의 가중치 변수를 많이 생성하고, 레이어를 깊게 쌓을수록 해당 모델은 training data에 오버피팅될 가능성이 높다. 오버 피팅을 해결하기 위해서 1. training data를 더욱 늘리거나 2. feature(x 변수)를 줄이거나 (이 방법은 굳이 사용하지 않아도 괜찮다.) 3. Regularization(정규화)를 진행해 모델의 하이퍼플레인(선)을 보다 평탄하게 해주는 방법이 있다. (= 가중치에 너무 큰 값을 배정하지 않게 하자!)
# 드롭아웃 (Dropout)
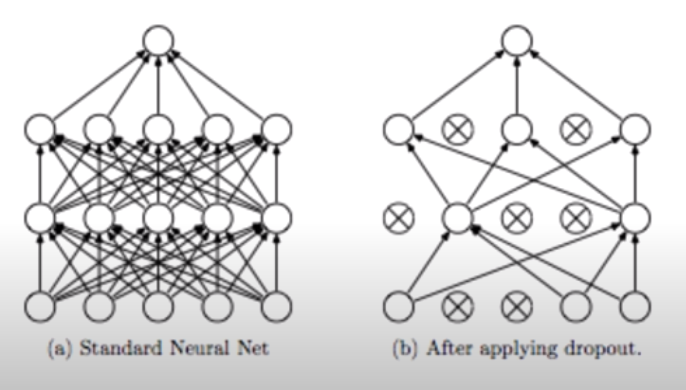
그러나 뉴럴넷 모델이 복잡해지면 정규화만으로 오버피팅에 대응하기 어려워지는데, 이 때 Dropout 기법이 사용된다. Dropout: A Simple Way to Prevent Neural Networks from Overfitting (Nitish Srivastava et al. 2014) 논문에 따르면 Dropout은 랜덤하게 어떤 뉴런들의 연결을 끊고 해당 뉴런을 비활성화시켜 뉴럴넷을 보다 간소하게 만드는 방법이다. 힘들게 만든 뉴런들을 왜 없애는 지에 대한 강한 의문이 들 수 있지만, 이 방법은 생각보다 큰 성능 상승 효과를 가져온다.
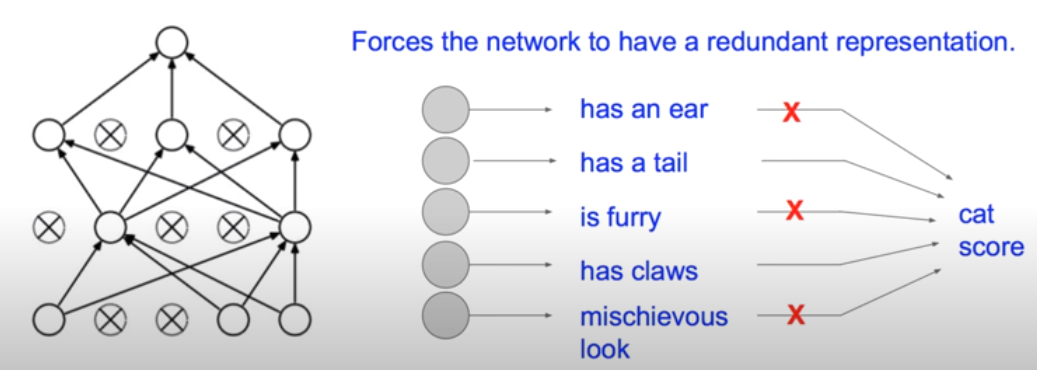
각 뉴런들은 각자 한 분야의 전문가 역할을 한다. 예를 들어, 고양이인지 아닌지 판단하는 뉴럴 넷을 사용한다고 할 때, 어떤 뉴런은 귀를 갖고 있는지 아닌지 판단하는 전문가, 어떤 뉴런은 꼬리를 가지고 있는지 판별하는 전문가, 어떤 뉴런은 털이 있는지 없는지 판단하는 전문가이다. 이런 뉴런들 중 몇몇을 쉬게 하여 학습을 진행하는 것이 Dropout 방법이다.
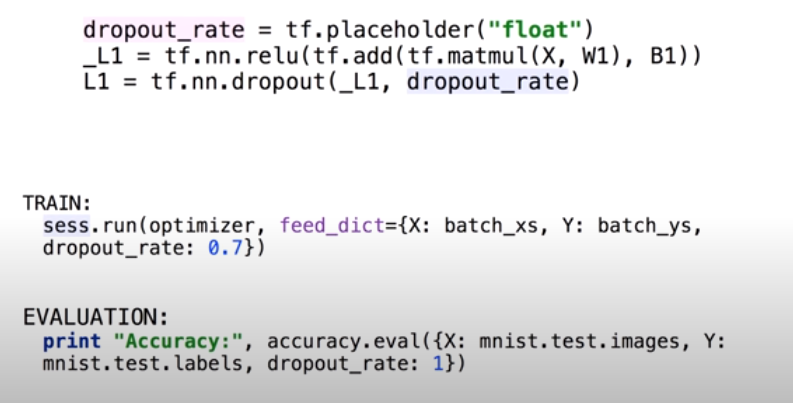
Dropout을 텐서플로우에서 적용하는 방법은 단순히 활성화 함수까지 있는 레이어에 Dropout 레이어를 하나 추가해주는 것이다. 이 때 dropout_rate를 설정해줘야 하는데, 보통 0.5로 설정하여 매 레이어마다 랜덤하게 학습하는 뉴런을 다르게 한다. Dropout에서 주의할 점은 training할 때만 적용해야 한다는 점이다. 학습시킬 때는 Dropout으로 랜덤하게 뉴런들을 학습시키고 test할 때는 dropout없이 모든 뉴런을 사용해서 예측해야 한다.
# 앙상블 (Ensemble)
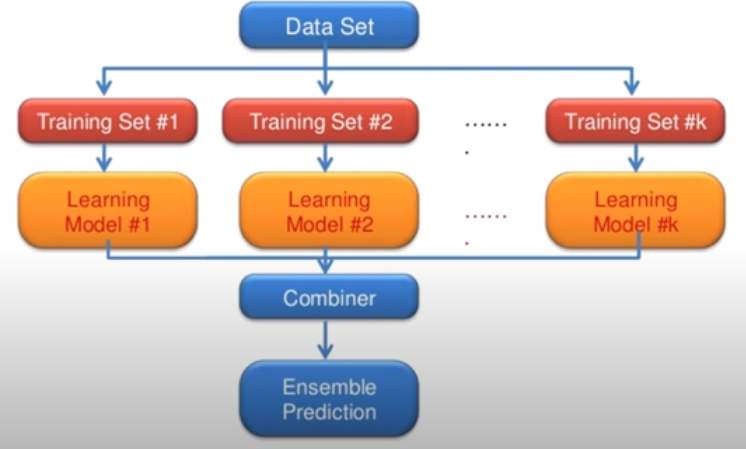
모델의 성능을 높이는 방법 중 하나로 앙상블(Ensemble) 기법이 있다. 예를들어, 위 그림과 유사하게 9개의 층을 가진 신경망 모델이 k개 있다고 하면, 이를 각각 모두 학습시킨 후 예측한 결과들을 마지막에 통합하여 최종적인 예측 결과를 도출할 수 있다. 마치 여러 전문가에게 의견을 물은 후 투표를 통해 최종적인 결론을 내리는 것과 유사한 이 방법은 적게는 2%에서 많게는 4~5%까지 모델의 성능을 향상시킨다.
CNN (Convolutional Neural Network)
# CNN (Convolutional Neural Network)
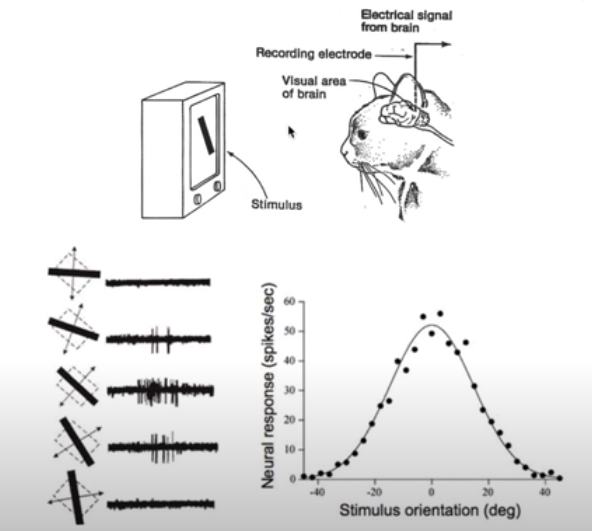
CNN의 시작은 고양이의 시각 인식에 관한 연구에서 비롯됐다. 고양이가 어떤 사진을 인식할 때, 각 뉴런이 각각 자신이 맡은 사진의 특정 부분에만 활성화되는 것이 확인되었고, 컴퓨터의 이미지 인식에도 같은 방식을 적용하는 시도가 이뤄졌다.
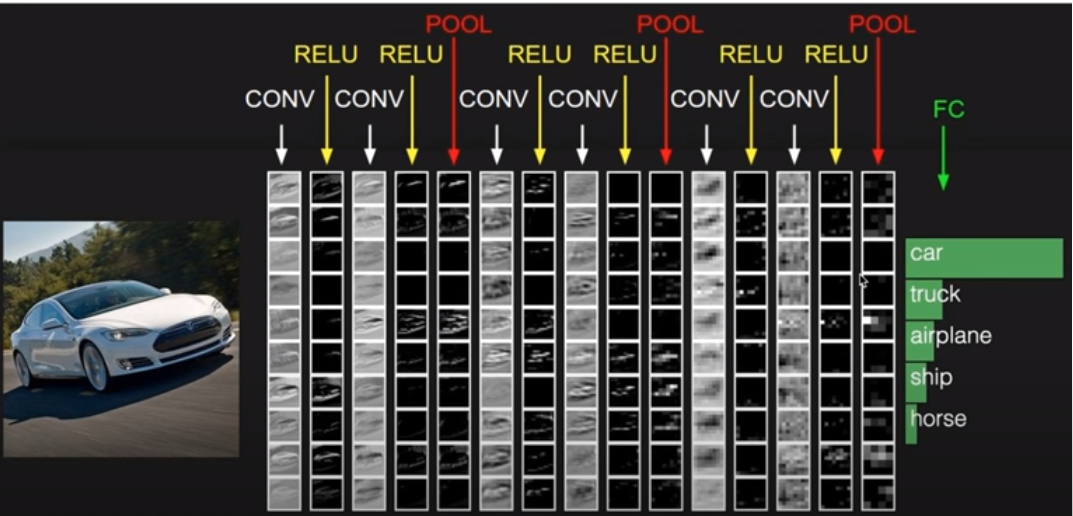
CNN은 Convolutional Layer와 ReLU, Pooling 계층의 반복적 조합으로 구성되며 끝에는 Fully Connected Layer로 결과를 분류한다.
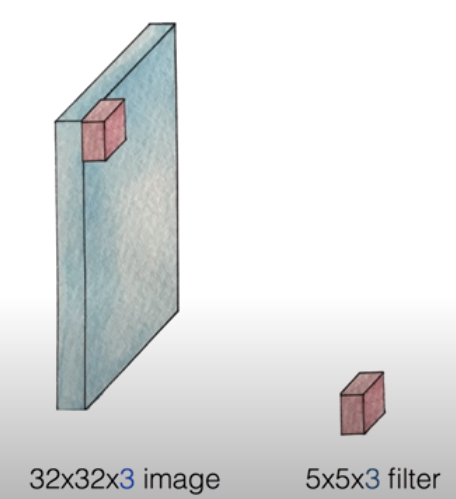
실제로 CNN을 동작시킬 때, 행렬의 크기 단위로 설정한 filter를 사용해 전체 이미지를 부분으로 쪼개어 처리한다. 위 그림의 예는 3개의 RGB 컬러로 구성된 32 pixel X 32 pixel 이미지를 5 X 5 X 3의 크기를 가진 filter로 처리하는 모습이다.

Filter는 원래 딥러닝에서 사용하던 Wx + b 회귀식의 가중치 행렬 W로 표현된다. 따라서 이미지를 filter를 통해 처리하는 것은 쪼개어진 이미지를 회귀식을 통해 계산해 하나의 숫자 ouput으로 만드는 과정을 의미한다. 이 과정을 쪼개어진 이미지 모두에 적용하면, 우리는 보다 축소된 크기의 숫자값 행렬을 얻을 수 있다. 이러한 과정을 거쳐 얻은 행렬을 Feature map이라고 하고 이 피쳐맵에 활성화 함수를 적용한 것을 Activation map이라고 한다.
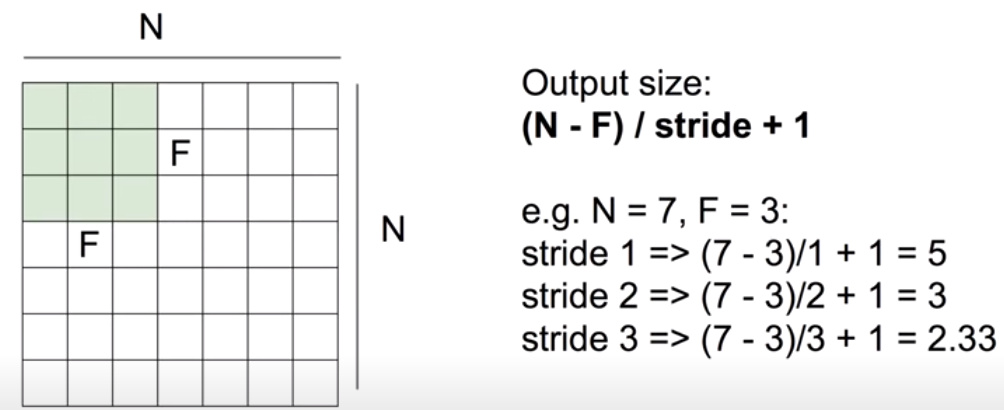
그렇다면 Feature map 하나의 크기는 어떻게 될까? 위 그림의 공식처럼 Output의 행 혹은 열 길이는 (N - F) / stride + 1로 구할 수 있다. 여기서 Stride는 filter를 몇 칸씩 이동하며 적용할지를 나타낸다. 예를들어, 위 그림에서 이미지의 가로, 세로 길이를 N이라 하고 filter의 가로, 세로 길이를 F라 한다면, N = 7, F = 3이다. 따라서 stride를 1로 설정해 filter를 한 칸씩 이동하며 적용하는 경우에는 (7 - 3) / 1 + 1 = 5를 통해 Ouput이 5 X 5 크기의 행렬이 되고, stride를 2로 설정해 filter를 두 칸씩 이동하며 적용하는 경우에는 (7 - 3) / 2 + 1 = 3을 통해 Output이 3 X 3 크기의 행렬이 된다. Stride가 3인 경우에는 공식에서 정수로 나누어 떨어지지 않기 때문에, CNN 적용이 불가능하다.

그러나 filter를 통해 이미지를 축소시키는 것은 다시말해 어떠한 정보를 잃어버리게 된다는 점을 의미한다. 따라서, 일반적으로 CNN을 사용할 때는 이미지 가장자리에 0을 둘러싸는 Zero padding 처리를 한 후 진행한다. Zero padding을 진행하면 1. 이미지의 과도한 축소를 막을 수 있고 2. 이미지 모서리 부분의 위치를 어떤 형태로든 network에 알려줄 수 있다. 위 그림처럼 7 X 7 크기의 이미지에 1 pixel만큼 Zero padding 처리를 해 9 X 9 크기의 행렬을 만들면, 1만큼 stride를 적용해 3 X 3 크기의 filter를 거쳐 나오는 output의 크기는 (9 - 3) / 1 + 1 = 7을 통해 원래대로 7 X 7 행렬이 된다.
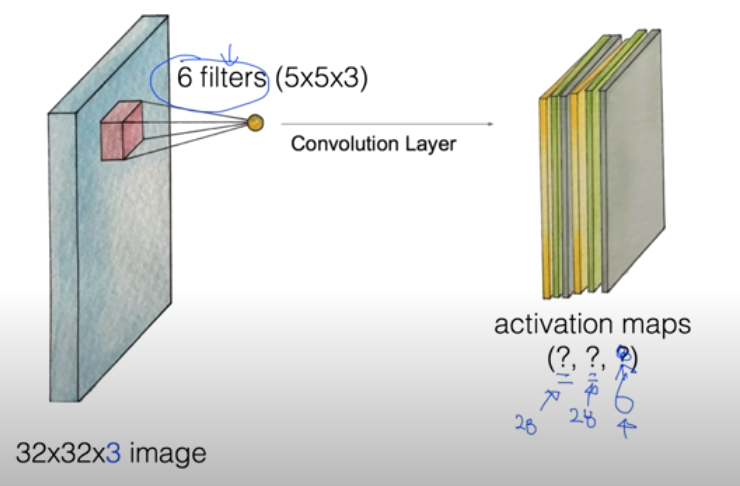
지금까지 Convolutional Layer에서 하나의 Feature map을 만드는 과정을 살펴봤다. 이후에는 이 과정을 각 가중치가 서로 다른 여러 개의 filter에 대해 적용해 여러 개의 Activation map(활성화 함수가 적용된 Feature map)을 하나의 Convolutional Layer에서 만들 수 있다. 위와 같이 가중치가 서로 다른 6개의 5 X 5 X 3 filter를 사용한다면, 총 6개의 28 X 28 크기의 Activation map을 만들 수 있다.
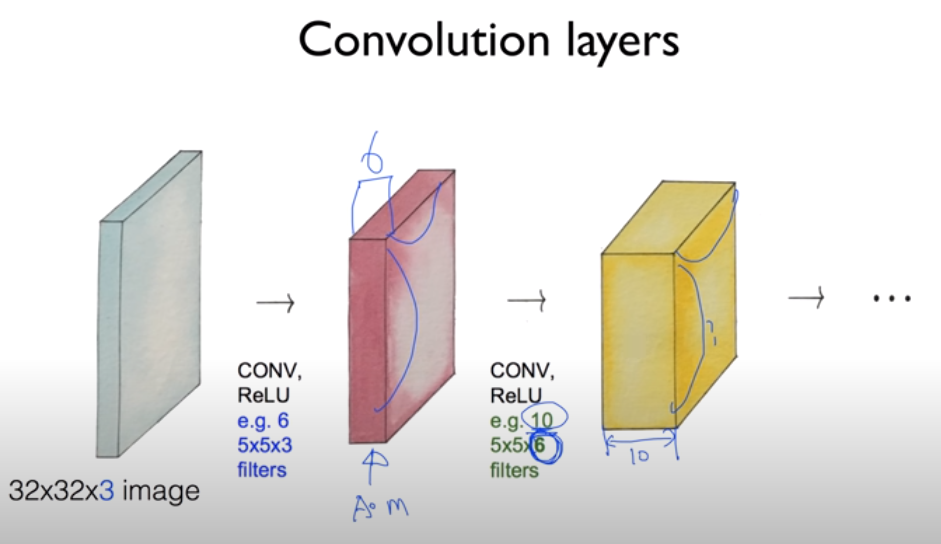
앞의 과정을 반복하면 위와 같이 여러 개의 Convolutional layer들을 만들 수 있다. Zero padding 없이 32 X 32 X 3 크기의 이미지를 첫 번째 Convolutional Layer에 넣으면 6개의 5 X 5 X 3 filter에 의해 28 X 28 X 6 Activation Maps가 나오고, 이를 두 번째 Convolutional Layer에 넣으면 10개의 5 X 5 X 6 filter에 의해 24 X 24 X 10 Activation Maps가 나온다.
참고로 각각의 layer에서 사용되는 weight의 개수는 그 layer에 적용되는 필터의 크기와 갯수를 곱한 값과 같다. 즉, 첫 번째 layer의 경우 크기가 5 X 5 X 3인 filter가 6개 존재하므로 weight의 개수는 450개이다.
# Max pooling과 Fully Connnected Layer
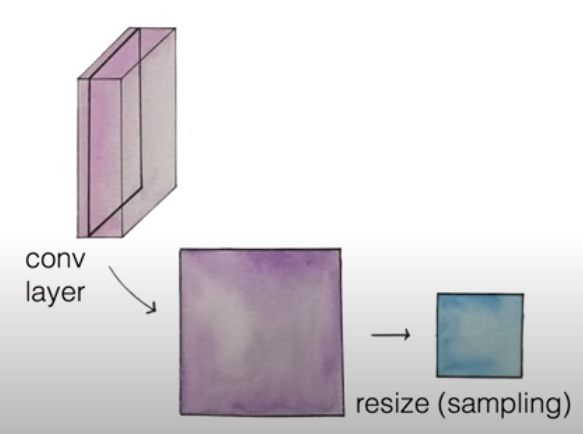
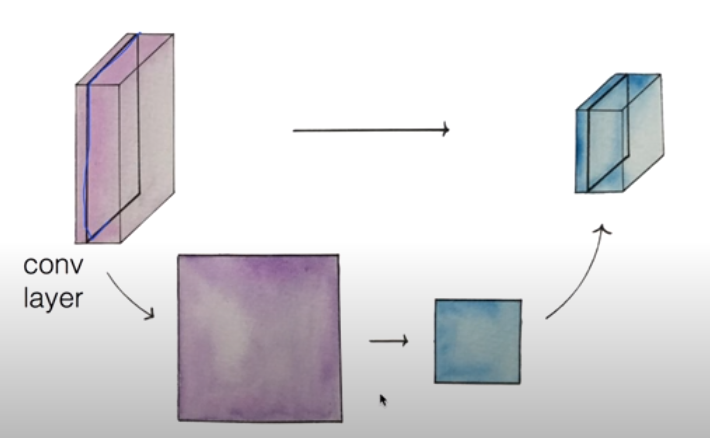
Pooling Layer란 하나의 Convolutional Layer에서 1개씩 부분 layer를 뽑아서 sampling을 통해 resize하여 다시 축소된 Convolutional Layer로 재구성한 Layer이다.
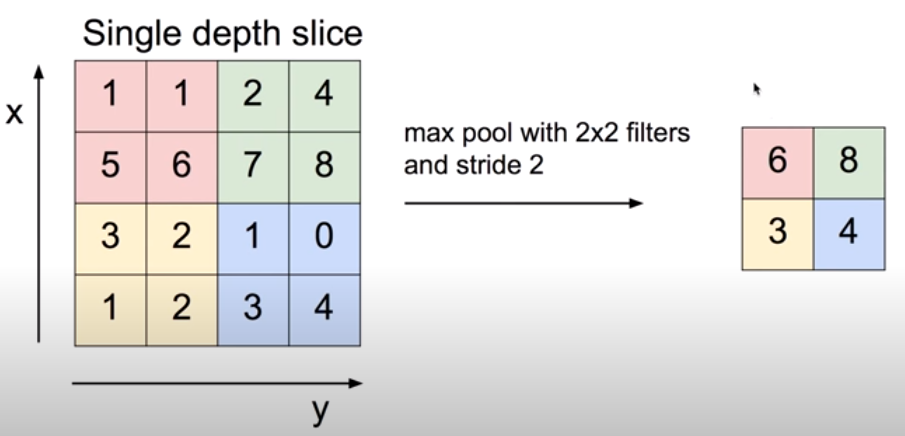
Pooling은 filter를 이용해 진행하는데, 보통 Max pooling이 자주 이용된다. 위 그림처럼 stride가 2인 2 X 2 크기의 filter가 있다면, 그 filter에 대상이 된 4개의 값 중 가장 큰 값 하나를 선택해 Pooling Layer의 요소로 사용한다. 따라서, 위 그림의 Pooling Layer 요소는 6, 8, 3, 4로 구성된다.
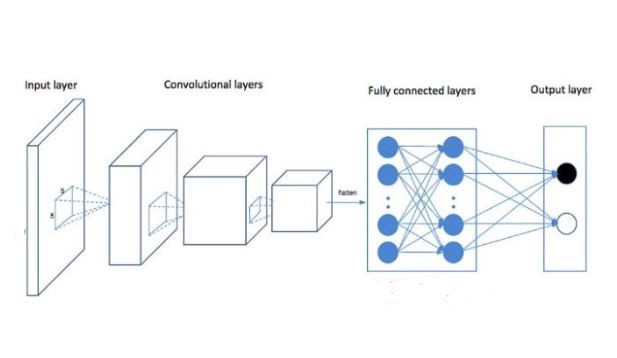
그리고 CNN 모델의 마지막에는 기존 Neural Network에서 사용하던 모든 뉴런들을 연결해 연산하는 Fully Connected Layer를 위치시킨다. Convolutional Layer의 경우 모든 뉴런을 연결시키지 않고 정보를 전달했는데, CNN의 끝 부분에서는 Softmax를 사용해 이미지를 분류해야 하므로 기존의 Fully Connected된 적당한 깊이의 Neural Network를 사용한다.
RNN (Recurrent Neural Network)
# RNN (Recurrent Neural Network)
출처: https://heung-bae-lee.github.io/2020/01/12/deep_learning_08/
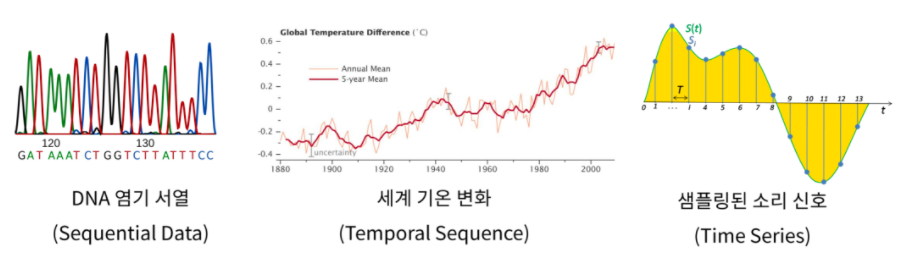
Data는 여러가지 종류가 존재하는데, 그 중 Sequential data의 처리는 기존의 Neural Net이나 CNN으로 해결할 수 없다. Sequential data란 순서에 의미가 있어서 순서가 달리지면 의미가 손상되는 데이터를 말한다. Sequential data에는 음성 인식에서의 소리 신호, 세계 기온 변화 추이와 사례가 있는데, 특히 언어의 경우 문장은 하나의 단어뿐만 아니라 그 앞뒤의 단어들까지 고려해야 이해가 가능하다. 이러한 Sequential data를 처리하는 기법으로 RNN(Recurrent Neural Network)이 사용된다.
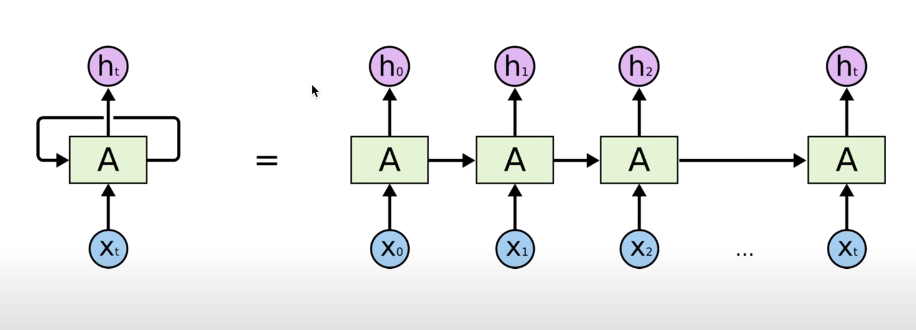
RNN에서는 입력으로 계산한 값이 그 다음 것에 영향을 주도록 구조화한다. 위 그림에서 입력 X0를 받아 Cell이라고 부르는 A에서 계산된 상태(state)를 그 다음 입력 X1으로 계산된 A에 전달하는 것이 이에 해당한다. 즉 어떤 시점에서 무언가를 계산할 때, 이전 시점의 것들이 영향을 미친다는 점에서 Sequential data를 처리하는데 적합하다.
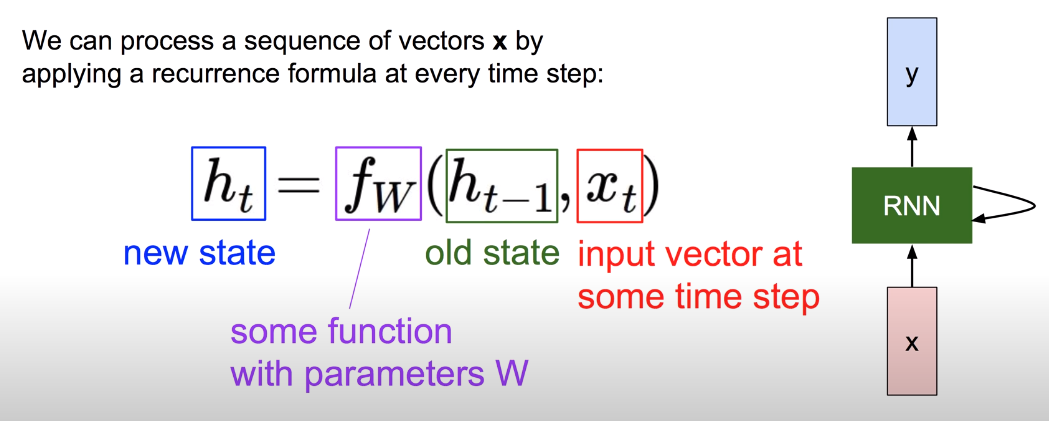
새로운 state를 연산하는 방법은 위의 공식과 같다. Input X와 이전 시점의 state에 가중치 W와 관련된 함수를 연산해주면 새로운 state의 값을 구할 수 있다. RNN에는 모든 state에 똑같은 공식이 적용되므로 위 그림의 모델처럼 순환 화살표 표시를한다.
# Vanila RNN
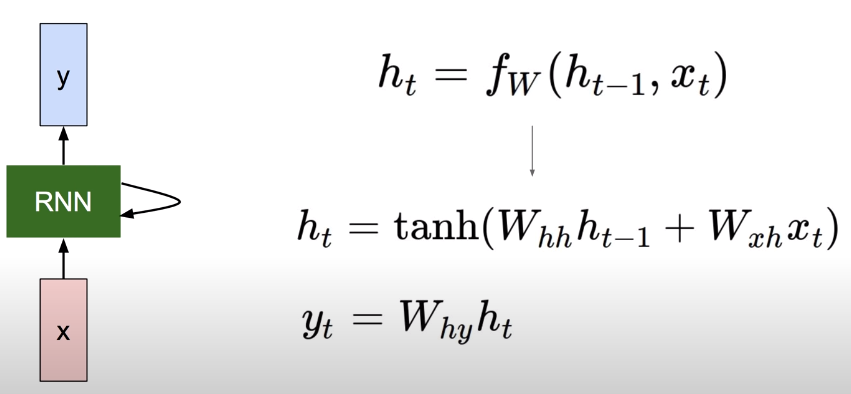
RNN의 가장 기본적인 형태는 위의 공식을 사용한다. 새로운 state를 연산하기 위해 이전 state와 input X에 각각 다른 가중치를 기존 회귀식같이 WX형태로 곱해주고 두 값을 더한다. 그리고 더한 값에 tanh 함수를 활성화함수로 사용해 새로운 state를 구한다. Output Y를 구할 때도 비슷하게 또 다른 가중치 W를 기존 WX 형태로 곱해주면 된다.
이 연산에서 사용하는 가중치 Wh, Wxh, Why는 어떤 state를 구할 때라도 항상 같다는 점을 주의하자.
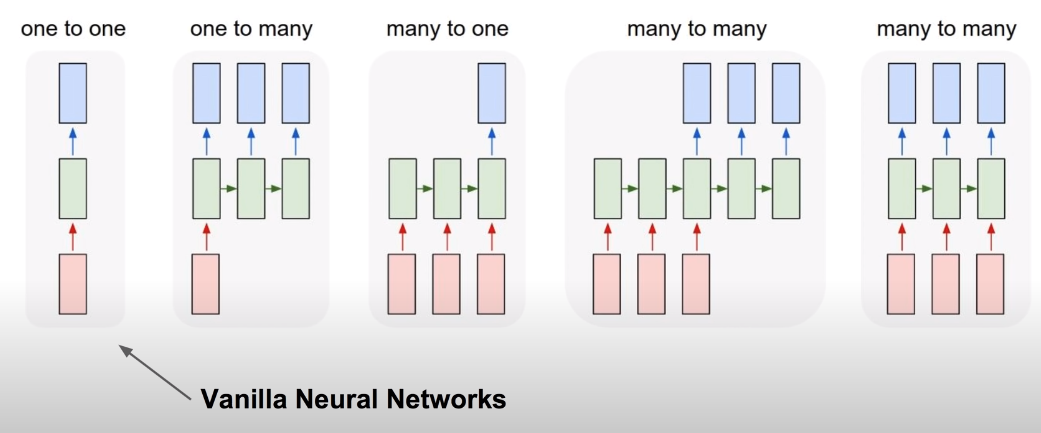
단순한 신경망은 표현력에 한계가 있지만 RNN을 사용한다면 활용 범위가 크게 넓어진다.
· One to Many: Image Captioning (이미지를 인식하여 여러개의 문자열로 표현하는 분야)
· Many to One: Sentiment Anlaysis (여러 개의 문자열을 입력 받아 하나의 감성을 나타내는 문자열로 분석하는 분야)
· Many to Many: Machine Translation (여러 개의 문자열을 입력 받아 여러 개의 문자열로 번역하는 분야)
· Many to Many: Video Classification on frame level (여러 프레임을 입력 받아 여러 개의 문자열로 표현하는 분야)
이러한 방식으로 RNN도 다양한 형태를 띌 수 있는데, RNN이 보다 깊어지고 복잡해질수록 기존 신경망 모델과 마찬가지로 학습이 어려워지는 현상이 발생한다. 이를 극복하기 위한 Advanced Model로 조경현 교수님이 만든 GRU나 LSTM(Long Short Term Memory)이 존재한다.
# Hello의 예
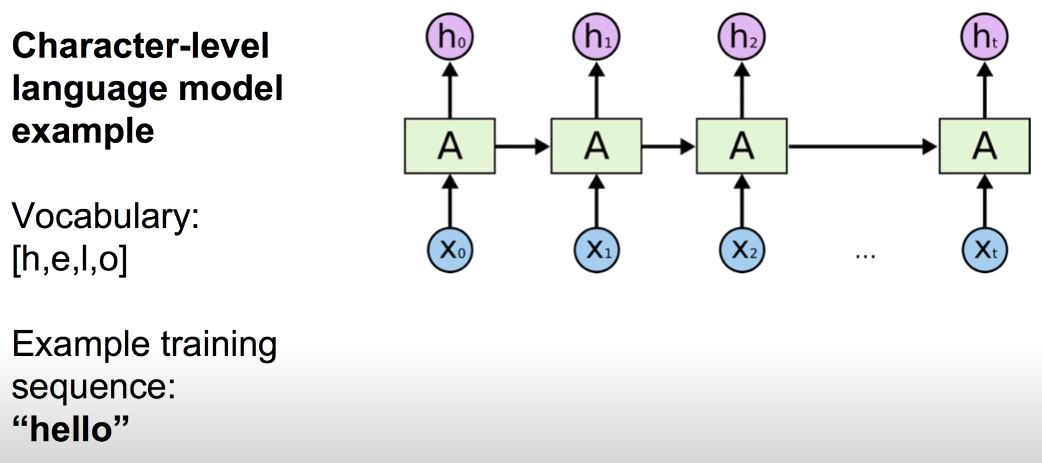
RNN 모델에 단어 ‘hello’를 학습시키는 예를 살펴 보자. ‘hello’는 철자 단위로 모델을 학습시킬 수 있다. X0에 ‘h’, X1에 ‘e’, X2에 ‘l’, X3에 ‘l’을 입력으로 넣고 입력된 철자 다음으로 나올 철자를 예측하도록 설계할 수 있다. 이 경우 h0는 ‘e’, h1은 ‘l’, h2는 ‘l’, h3은 ‘o’를 output으로 예측한다.
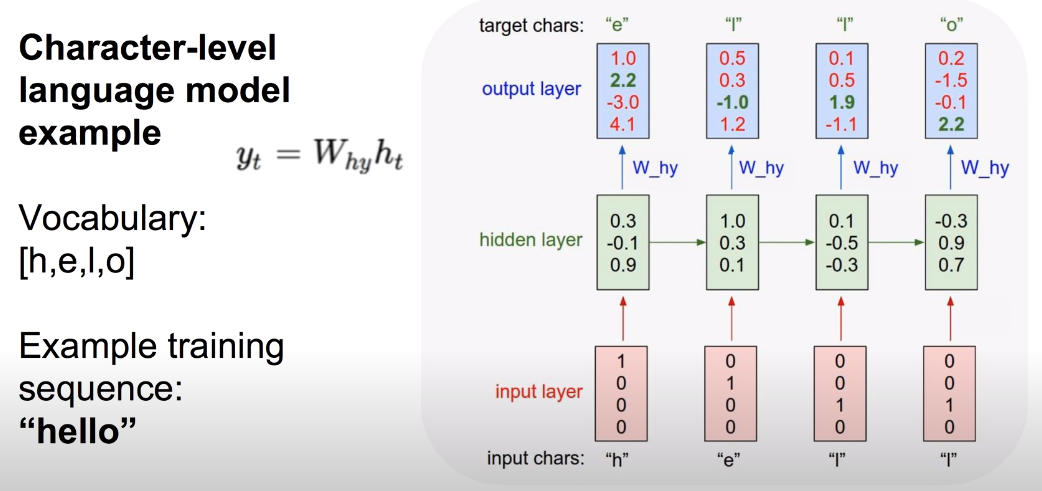
이 때, 위 그림처럼 고정된 값 Whh, Wxh, Why를 가중치로 사용하여 각 input의 state를 연산하고 output Y를 출력한다. Input X의 경우 one-hot 인코딩을 통해 철자를 표현하는게 일반적이고 output은 softmax를 통해 철자 예측을 진행하면 되는데, 모델의 학습 역시 기존의 softmax에 대한 cost 함수를 사용해 진행하면 된다.
본 포스팅은 김성훈 교수님의 강의
‘모두를 위한 딥러닝’을 학습하고 정리한 내용을 담고 있습니다.
