Machine Learning 개요

# 머신러닝이란?

 Explicit(=many rules)한 프로그래밍을 지양하고, 프로그램에게 데이터를 보고 스스로 학습할 능력을 부여해서 어떠한 결과를 도출하게끔 하는 연구하는 분야

→ Field of study that gives computers the ability to learn without being explicitly programmed (Arthur Samuel, 1959)

# 학습 방법에 따른 유형

1. Supervised learning

 : 컴퓨터에게 정답(label)이 무엇인지 알려주면서 학습시키는 방법 (label이 있는 data로 학습)

• Regression
  • 어떠한 연속된 값을 주어진 데이터들의 특징(feature)을 기준으로 예측하는 문제
  • ex) 시험공부에 투자한 시간에 대한 기말시험 ‘점수’ 예측
• Binary Classification
  • 주어진 데이터를 2개의 카테고리로 분류하는 문제
  • ex) 개와 고양이 구분
• Multi-Class(=Multi-Lable) Classification : 주어진 데이터를 3개 이상의 카테고리로 분류하는 문제
  • ex) 시험공부에 투자한 시간에 대한 기말시험 ‘등급’ 예측

2. Unsupervised learning

 : 정답(label)을 알려주지 않고 비슷한 데이터를 군집화하여 미래를 예측하는 학습 방법 (label이 없는 data로 학습)
 ex) Google news grouping, Word clustering

• Clustering
• Dimensionality Reduction
• etc…

Linear Regression

# Linear Regression

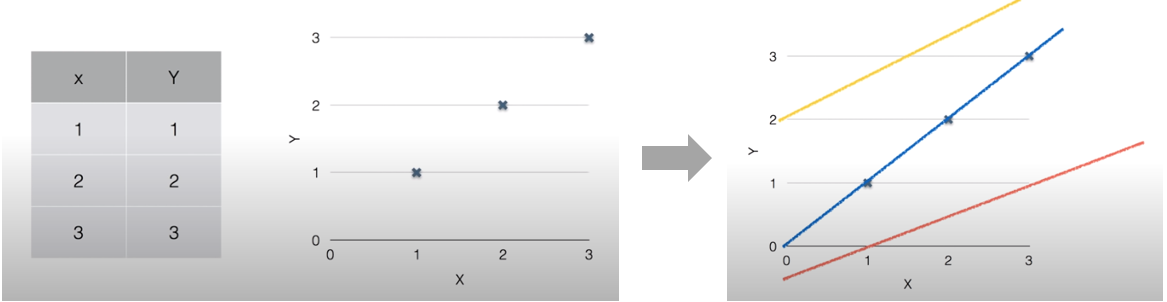
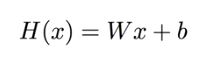
 주어진 학습 데이터를 가장 잘 설명할 수 있는 선을 찾아 분석하는 방법이다. (Regression은 연속하는 값을 가지는 학습 데이터에 한해 사용한다.) 위 그림처럼 주어진 데이터를 그래프에 표현하고 여러가지 선을 긋다보면 파란선이 해당 데이터를 가장 잘 표현함을 알 수 있다. 이러한 선을 H(x) = Wx + b의 형태의 수식으로 찾아내는 것을 Linear Regression이라고 한다. 위 그림의 파란선은 H(x) = x로 나타낼 수 있다.

# Loss & Cost function

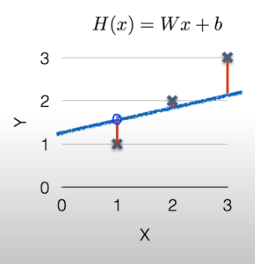
 Cost function은 예상한 가설(선)이 데이터에 얼마나 잘 맞는지 확인하는 함수이다. 보통 예측값에서 실제값을 뺀 값의 제곱인 (H(x) - y)²을 Loss로 사용하여 Cost function을 구한다. 

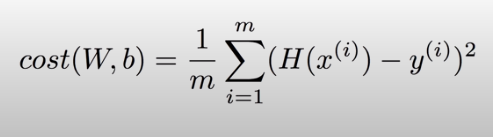
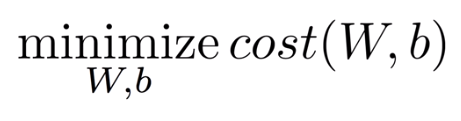
 즉 이렇게 계산한 모든 Loss의 평균을 내면 Cost function을 구할 수 있다. 딥러닝에서는 주로 이 Cost function이 사용되고 이러한 Cost function을 최소화시키는 W, b를 찾는 것이 목표가 된다.

Multi-variable linear regression

# Mulit-variable linear regression

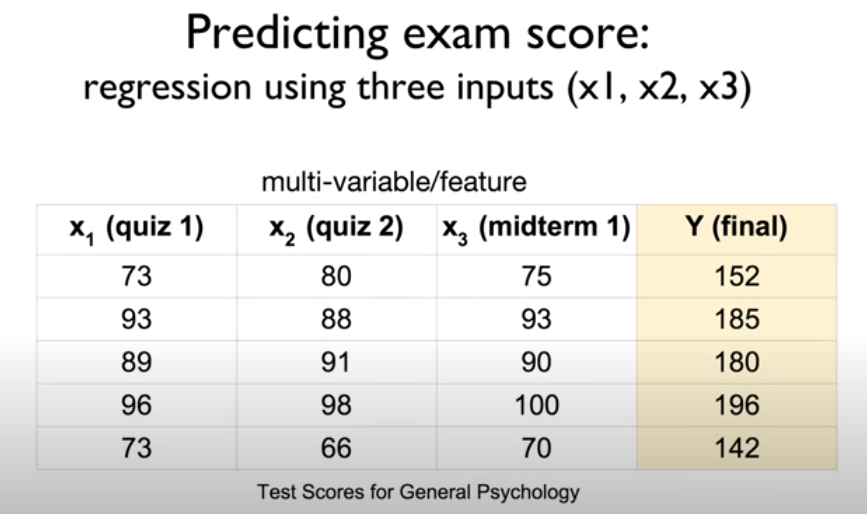
 앞에서 공부했던 선형 회귀는 하나의 변수에 대하여 출력을 계산했다. 그러나 위 시험 점수 예측 사례의 퀴즈 1 점수, 퀴즈 2 점수, 중간고사 점수처럼 여러개의 변수를 고려하여 회귀를 진행할 땐 어떻게 해야할까?

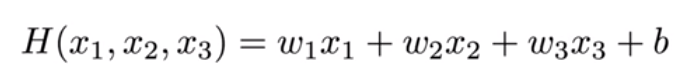
 기존의 선형 회귀 식은 H(x) = Wx + b였다. 다변량 선형 회귀는 위와 같이 기존 선형 회귀와 유사하게 새로운 가중치 w를 각각의 새로운 변수 x들에 곱해주면 된다.

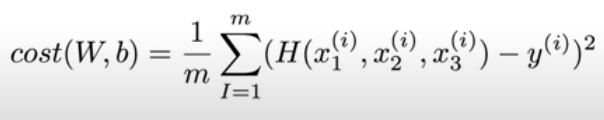
  다변량 선형 회귀의 비용함수 역시 선형 회귀의 비용함수 식을 그대로 가져오되 Hypothesis만 다변량 회귀식으로 적용하여 사용한다.

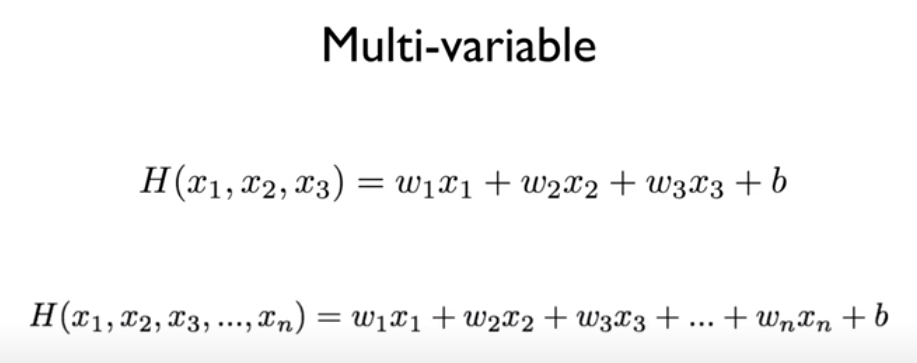
 Hypothesis를 n개의 변수에 대하여 일반화하면 위와 같다. 그러나 n의 값이 커질수록 식이 길어서 이를 표현하기 어려워지는 문제가 생긴다.

 식이 길어지는 문제는 행렬(Matrix)을 도입하는 방법(= Vectorization)으로 해결할 수 있다. 변수 x들에 대한 행렬 X와 각각의 변수에 대한 가중치 w들을 표현하는 행렬 W를 사용해 H(X) = XW라는 Hypothesis를 사용할 수 있다. 일반적으로 이론에 사용되는 식에서는 H(x) = Wx 처럼 W를 앞에 사용하지만, 실제로 구현할 때는 XW와 같이 X를 앞에 두고 사용한다. Vectorization은 n개의 변수에 대해 n번이나 수행되어야 하는 계산을 한번으로 줄여 효율적인 계산을 돕는 이점이 있다.

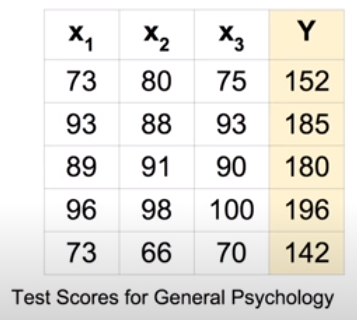
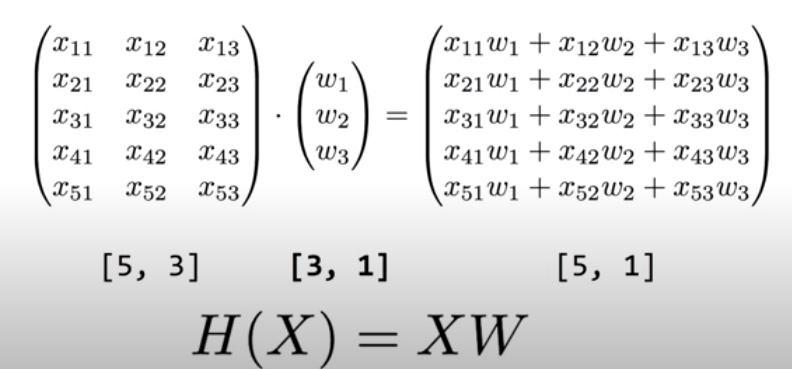
 위는 기말 시험 점수를 예측하는 다변량 선형 회귀에 대한 예시이다. 왼쪽 상단의 표에는 3가지 시험 점수 변수와 기말 점수 변수에 대한 데이터가 5개 있다. 이러한 데이터 하나하나를 Instance라고 한다. 행렬로 다변량 선형 회귀를 수행할 때는 그 행과 열에 정보가 담겨 있는데, X의 행은 instance의 개수(data의 개수), 열은 독립변수의 개수를 나타낸다. W의 행은 독립변수의 개수를 나타내며 열은 출력 개수를 나타낸다. 그리고 두 행렬 X와 W를 계산한 결과를 담는 행렬은 행이 instance의 개수, 열이 출력의 개수를 나타낸다.

Logistic Regression

# 이진 분류 (Binary classification)

 이진 분류(Binary Classification)는 어떤 문제에 대하여 두 가지 중 하나를 결정하는 문제이다. 메일이 스팸메일인지 아닌지, 페이스북 피드를 보여줄지 말지, 방금 진행한 신용카드 거래가 사기인지 아닌지 판단하는 것이 이진 분류의 예다. 일반적으로 결정해야할 두 가지 결과는 0, 1로 인코딩해 사용한다.

# 로지스틱 회귀 (Logistic Regression)

 1. 로지스틱 회귀와 시그모이드(Sigmoid) 함수

  이진 분류를 가장 잘 해결할 수 있는 방법으로 로지스틱 회귀(Logistic Regression)가 있다. 기존의 선형 회귀는 시험에 통과할 사람을 정확히 예측하는게 어렵고, 입력값이 커질수록 출력값이 0~1 범위를 크게 벗어나 결과를 두 가지로 분류하기 어렵다. 이러한 출력값을 0~1 범위로 압축하는 함수를 이용해 출력값을 분류하는 것이 로지스틱 회귀이다.

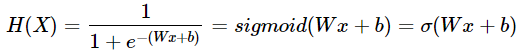
  로지스틱 회귀에서는 0~1 범위로 출력값을 압축하는 함수로 시그모이드(Sigmoid) 함수를 사용한다. 시그모이드 함수는 모든 출력값이 0~1 사이에서 나오는 특징이 있다. 이를 통해, 기존 가설인 선형 회귀에 시그모이드 함수를 덧입혀 이진 분류에 적합한 새로운 가설 H(x)를 만들 수 있다.

 2. 로지스틱 회귀의 Cost 함수

  기존 선형 회귀의 cost 함수는 기울기가 0이 되는 값이 하나여서 쉽게 최솟값을 찾을 수 있었지만, 로지스틱 회귀의 경우 비선형 함수인 sigmoid 함수로 인해 cost 함수가 훨씬 구불구불한 형태를 띄게 된다. 이로 인해, 기울기가 0이 되는 지점이 많아져 시작점에 따라 경사하강법으로 찾는 최솟값의 지점이 달라진다. 즉, cost 함수의 진짜 최솟값을 찾는 것이 어렵다.

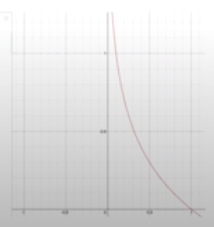
  이를 극복하기 위해, 로지스틱 회귀에서는 위와 같은 cost 함수를 사용한다. 가장 왼쪽에 있는 그래프는 y = 1일 때의 cost 함수, 그 옆에 있는 그래프는 y = 0일 때의 cost 함수이다. 시그모이드 함수로 인해 생기는 지수함수적 특성을 log 함수를 사용해 중화한 덕분에 전체적으로 포물선과 비슷한 형태를 띈다. 따라서, 최솟값 찾기가 용이하다. 

  cost 함수 그래프를 살펴보자. y = 1일 때의 그래프에서 H(x)가 1에 가까울수록(예측값이 정답에 가까울수록) cost 함수가 작아지고 H(x)가 0에 가까울수록(예측값이 틀릴수록) cost 함수가 무한대로 커진다. 반대로 y = 0일 때의 그래프에서 H(x)가 1에 가까울수록(예측값이 틀릴수록) cost 함수가 무한대로 커지고 H(x)가 0에 가까울수록(예측값이 정답에 가까울수록) cost 함수가 작아진다. 로지스틱 회귀의 cost 함수가 비용함수의 역할을 정확히 수행함을 확인할 수 있다.

  비용함수를 텐서플로우로 실제로 구현할 때는 C(H(x), y) = - ylog(H(x)) - (1 - y)log(1 - H(x)) 식을 사용한다. 위의 y = 1일 때와 y = 0일 때의 비용함수를 똑같이 표현한 같은 식이며 구현의 편의를 위해 사용한다.

Multi-Class Classification - Softmax

# 다중 클래스 분류 (Multi-Class Classification)

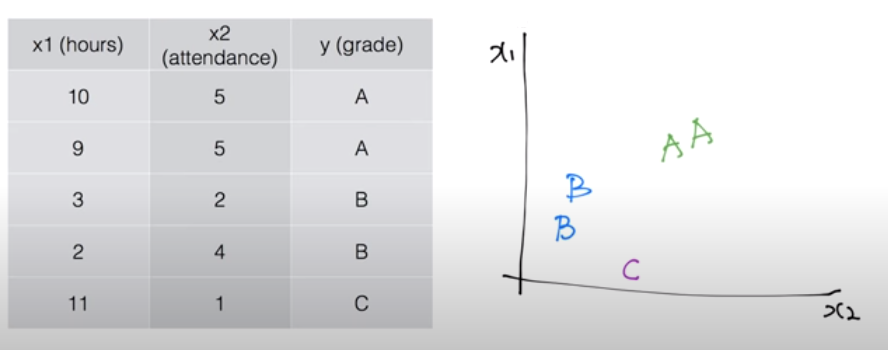
 앞선 로지스틱 회귀에서는 두 가지 선택지만 결정했다. 만약 세 가지 이상의 클래스를 두고 결정해야 하는 상황이라면 다중 클래스 분류(Multi-Class Classification)를 한다. 위와 같이 시간과 출석 여부라는 두 가지 변수에 대하여 A, B, C 세 가지 성적을 매기는 상황을 가정해보자. 성적 분포의 그래프는 오른쪽 그래프와 같다.

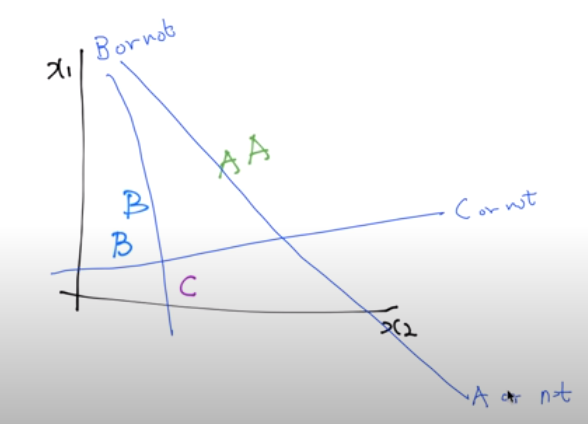
 성적이 표현된 그래프를 로지스틱 회귀를 사용한다고 생각하고 A에 대해, B에 대해, C에 대해 각각 이진 분류한다면 위와 같이 3가지 선을 그을 수 있다. A인지 아닌지, B인지 아닌지, C인지 아닌지를 구별하는 세 가지 선을 그은 것이다.

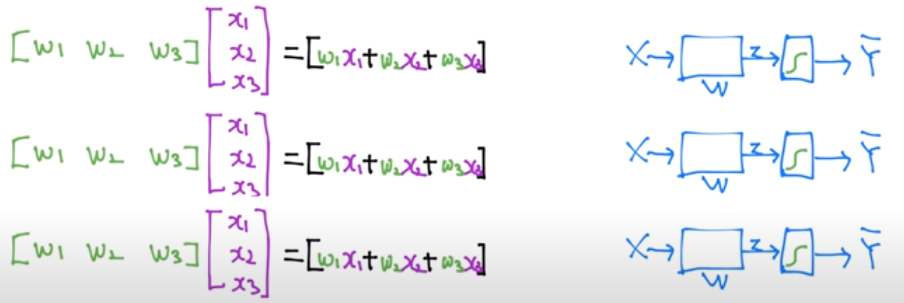
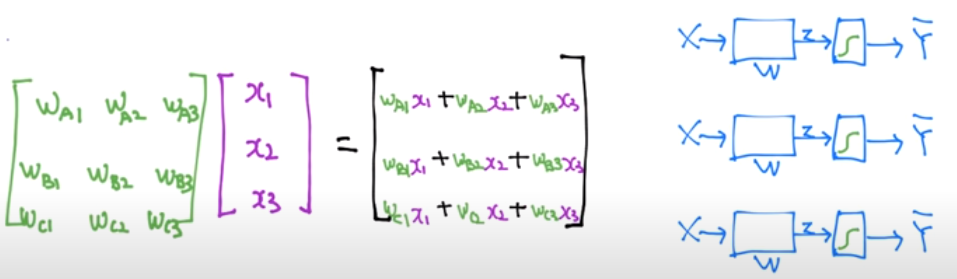
 이 3가지 식을 행렬로 표현하면 왼쪽 그림과 같다. 그리고 계산의 편의를 위해 이 식들을 또 하나의 행렬로 통합하면 오른쪽 그림과 같아진다. 오른쪽 그림의 계산식의 3가지 출력이 각각 A, B, C에 대한 H(x) 값이 된다.

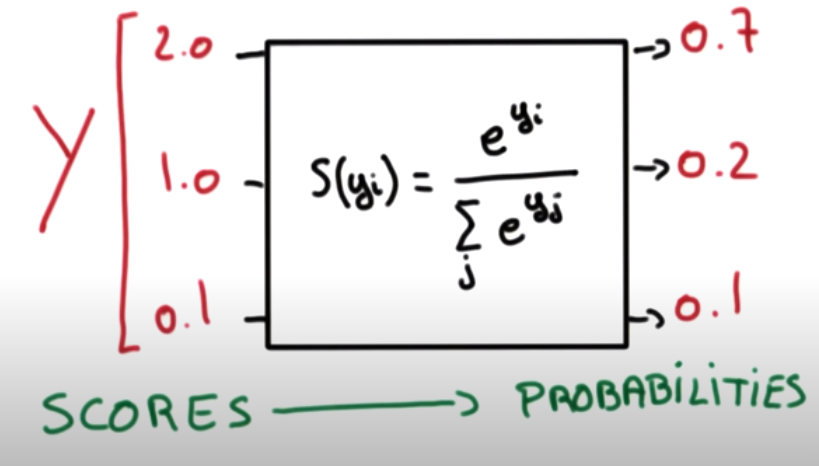
 A, B, C에 대한 각각의 예측값이 0~1 범위에 있게 하고 모두 합해 1이 나오게 한다면 편리한 계산을 할 수 있다. 이를 위해 위 그림과 같은 Softmax 함수를 사용한다. Softmax 함수를 사용하면 A, B, C에 대한 세 가지 예측값을 확률로서 사용할 수 있게 된다.

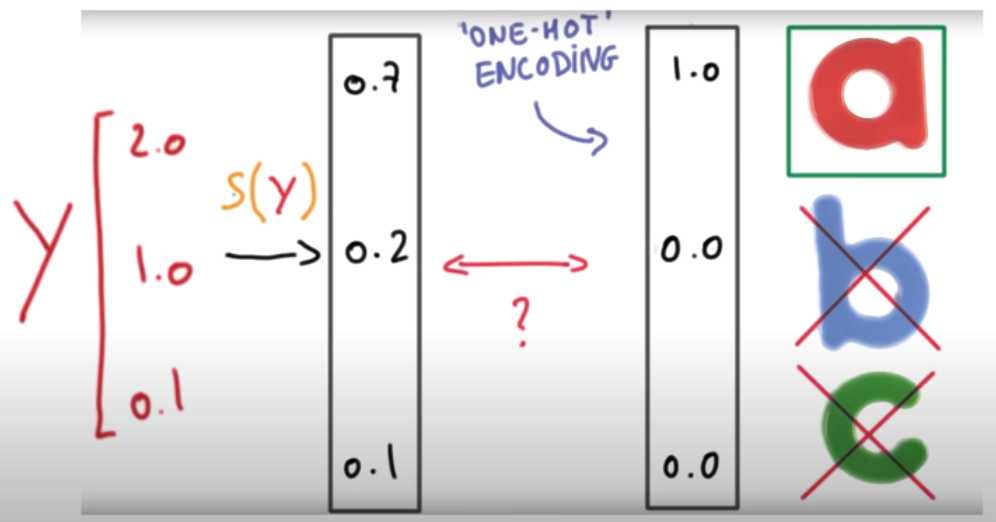
 Softmax로 도출된 각각의 확률은 One-Hot Encoding을 통해 1 혹은 0으로 분류되고 각각의 예측값이 결론적으로 가리키는 것이 A인지 B인지 C인지를 확인할 수 있게 된다.

※ Softmax의 Cost 함수

Learning rate, Overfitting and Regularization

# Learning rate (학습률)

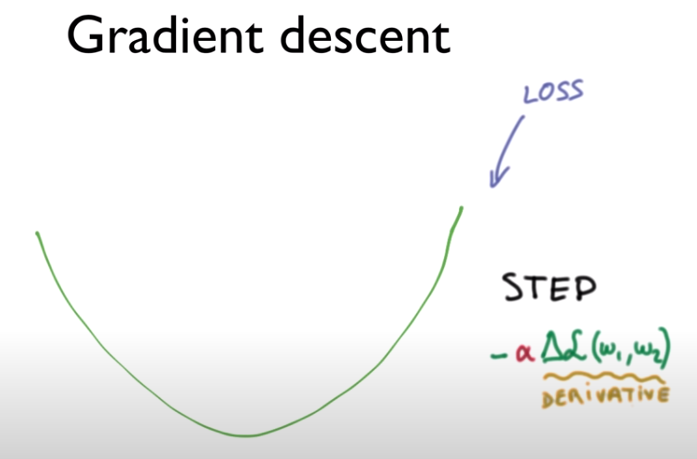
 Gradient Descent를 진행할 때, 각 step마다 어느 정도씩 진행할지 Learning rate(학습률)을 지정하여 설정할 수 있다. (위 그림에서 알파값이 학습률을 나타낸다.)

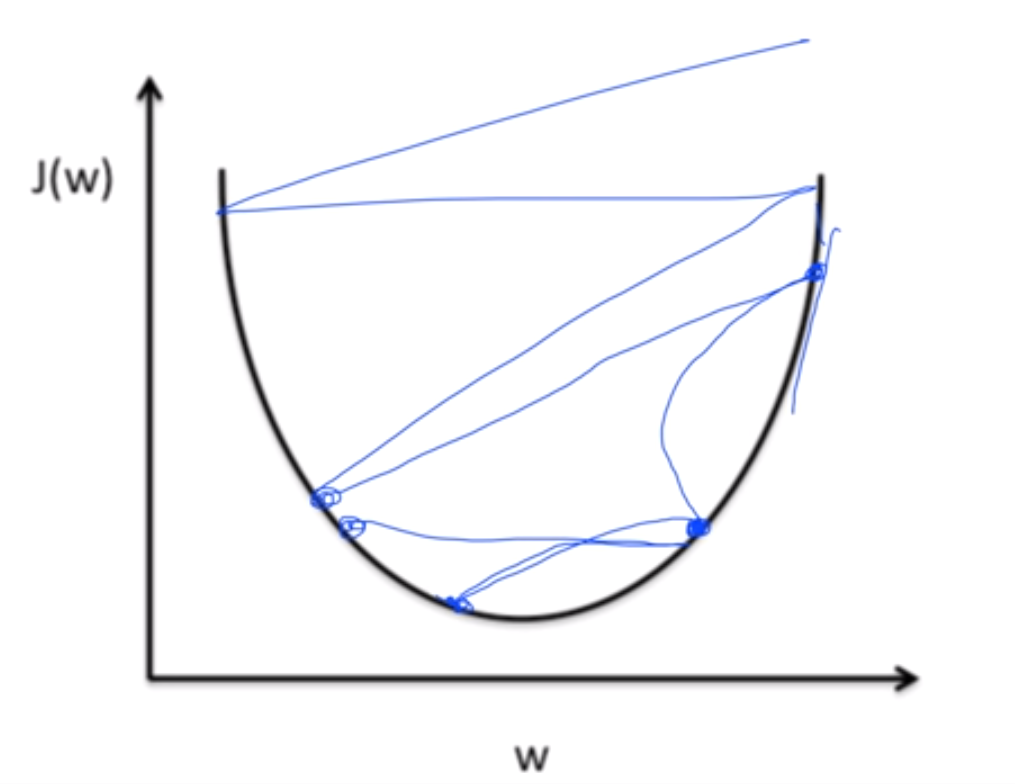
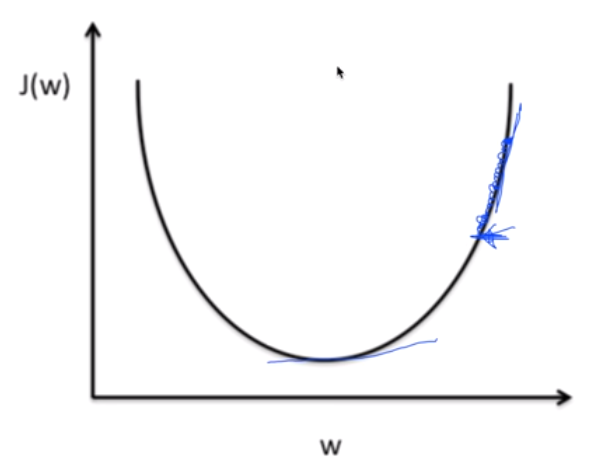
 학습률을 너무 큰 값으로 설정하면 스텝마다 큰 폭으로 학습이 진행되어 왼쪽 그림처럼 w값이 발산해버리는 오버슈팅(Overshooting) 문제가 발생할 수 있다. 반대로 학습률을 너무 작은 값으로 설정하면 스텝마다 작은 폭으로 학습이 진행돼 오른쪽 그림처럼 학습이 더뎌지는 문제가 발생한다. 학습률 설정에 정답은 없지만 처음에 0.01의 학습률을 설정하고 양상에 따라 조절하는 것도 한 방법이 될 수 있다.

# 데이터 전처리 (Preprocessing)

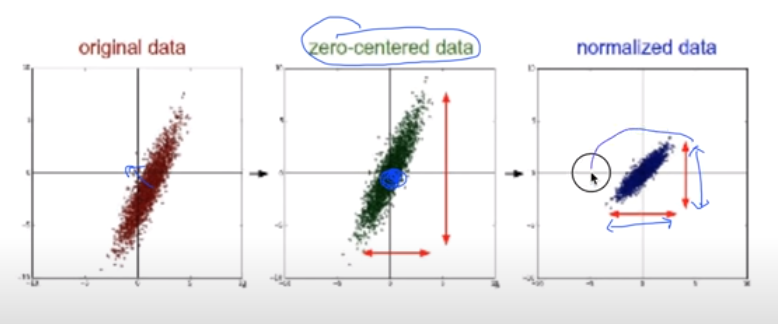
 데이터들을 다루다보면 x data에 해당하는 각각의 변수들의 값의 범위가 서로 크게 차이날 수 있다. 이러한 경우 적절한 학습률을 설정해도 오버피팅이나 언더피팅이 발생할 수 있는데, x data를 적절하게 전처리(Preprocessing)해주면 다시 정상적으로 학습시킬 수 있다. 이러한 전처리는 보통 zero-centered를 통해 원래의 데이터를 0을 중심으로 분포하게 만들거나, Normalization을 통해 변수 값의 범위를 특정 범위에 속하게 만드는 방법들이 있다.

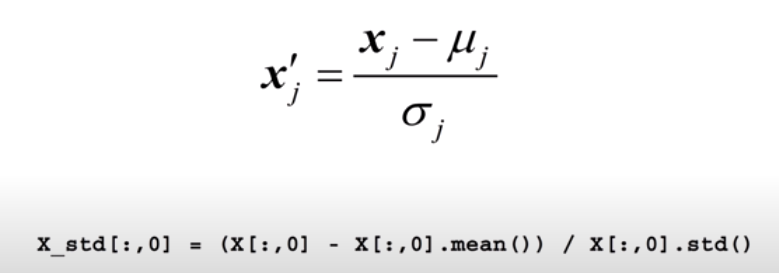
 이러한 normalize의 대표적인 예 중 하나가 표준화(Standardization)이다. 기존의 data에서 그 평균을 빼고 표준편차로 나눠주면 data는 표준정규분포를 따르게 되어 특정 범위 내에 분포하게 된다. 고등학교에서 통계 과목을 배울 때, 자주 봤던 이 개념을 사용해 data를 표준화시키면 정상적인 학습 진행에 큰 도움을 준다.

# 오버피팅 (Overfitting)

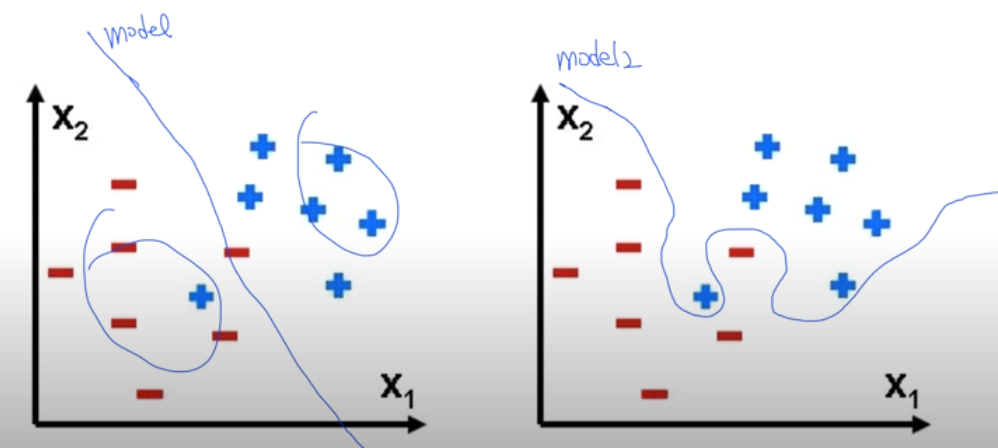
 학습시킨 모델이 training data(학습 데이터)에서만 너무 잘 맞아서 test data나 실제 문제에서는 좋은 성능을 발휘하지 못하는 현상을 오버피팅(Overfitting)이라고 한다. 오른쪽 그림은 학습 데이터에서 +와 -를 완벽하게 가르지만 실제 문제를 다룰 때는 +와 -를 나누는 성능이 왼쪽 그림에 비해 더 떨어질 수 있다. 이 경우엔 오버피팅 문제가 없는 왼쪽 모델이 더 성능이 좋으므로 모델을 학습시킬 땐 항상 오버피팅에 대해 경계해야 한다.

 오버피팅의 해결책으로는 1. training data를 더 많이 확보하는 것 2. feature의 개수를 줄이는 것(=x변수를 줄이는 것) 3. Regularization시키는 것 등이 있다.

# Regularization

 Regularization이란 데이터를 가르는 모델의 구불구불한 선을 조금 더 평탄하게 만드는 것을 의미한다. 보통 가중치 w의 값이 커질수록 모델의 선이 구불구불해지고, w의 값이 작아질수록 모델의 선이 평탄하게 뻗게 된다. 가중치 w 값을 보다 작게 하여 모델의 선을 적당히 평탄하게 만드는 Regularization을 통해 오버피팅을 어느정도 줄일 수 있다.

 Regularization은 cost 함수에 위 식을 더해주는 것으로서 구현하고 이를 L2 Regularization이라고 부른다. 맨 왼쪽의 람다 변수는 regularization strength라고 불리는데, 이 값이 0에 가까울수록 Regularization의 영향을 적게 한다는 의미고 이 값이 커질수록 Regularization의 영향력을 크게 한다는 의미이다. 이를 통해 가중치 값을 낮추고 오버피팅을 어느정도 극복할 수 있다.

본 포스팅은 김성훈 교수님의 강의
‘모두를 위한 딥러닝’을 학습하고 정리한 내용을 담고 있습니다.